Complex Parkour for Bots in Minecraft

A few years ago I created SwarmBot, an autonomous bot launcher for Minecraft in Rust. I called it Swarmbot because it is capable of launching hundreds of bots, each one on a separate SOCKS5 Socket, which is nice for servers like 2b2t, where I launched about 200 of them at once (this is ethical and within the server rules).

One of the main components of SwarmBot is its ability to parkour as seen in this video

It might seem like the bot posseses a superpower being able to do relatively complex jumps with ease, but it is really just a block-level A* and then a really well find-tuned algorithm that takes a list of blocks and figures out which actions (run, look, jump, etc) it should perform based on the direction and distance of the next block the bot needs to reach.

This works well 99% of the time, but it isn’t a guarentee the bot will work, and there are some cases the bot will not really be able to succeed without A LOT of spaghetti code—say for complex jumps like neos.

Neo jumps are especially complex because it doesn’t involve looking towards the next block in the sequence of blocks that need to be jumped to. Instead, it involves jumping around a block (facing away from the block to be jumped to) before finally looking at the block.

I had to implement physics on the client side to get the bot to behave like a normal player and to be able to be used on servers with NoCheatPlus. Therefore, I figured why not use physics to instead of discretize based on block to instead of discretize based on gametick and have children nodes be based on keys the player could press.

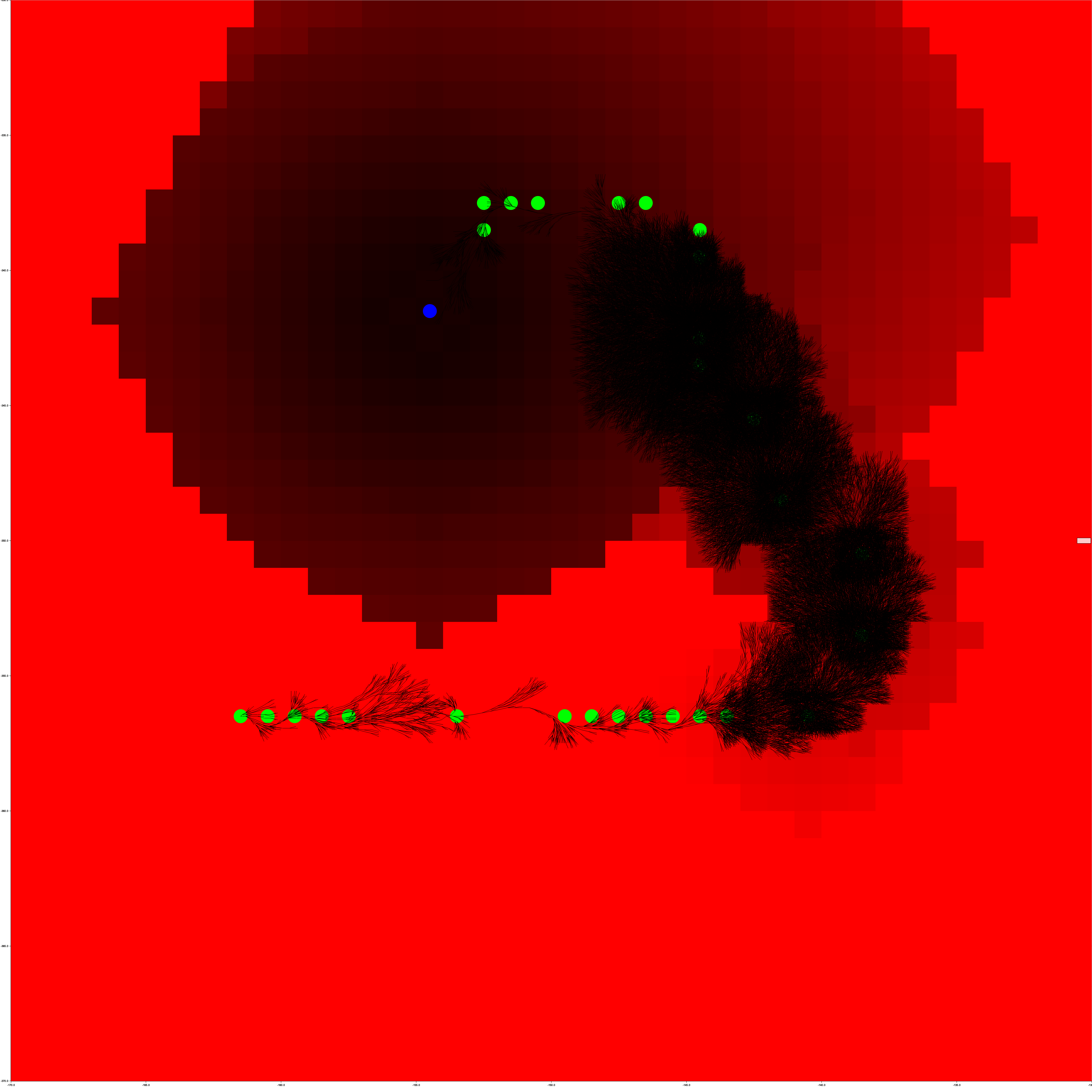
Below is the same parkour course as in the video above. Each green circle is a block and each node explored is black. No heuristic is used (unlike in the video) and the following options are

• run forward (cost 1)
• run forward and jump (cost 1)
• run forward and turn left 15º (cost 10)
• run forward and turn right 15º (cost 10)

As you can see there is a big issue. When the bot looks at possible turns, lower g-scores are taken into account first when really the ones that need to be tried are those furthest along (highest g-scores). My guess it would take until the end of the universe for this problem to finish. Potentially there is some great heuristic I can use, but I can’t think of one.

RTT #

Trying the same thing with RTT I get what is seen below. This is also not sufficient. RTT has several issues. It is useful for non-holonomic systems, say cars or—in this case—where the next neighbor states are not only locality based but also involve velocity, so a positional grid cannot be expanded in the same way positional A* will work. Non-holonomic systems struggle with A* because even if we consider a state $(x,y, \delta x, \delta y)$, where $(\delta x, \delta y)$ is the change in $x$ and $y$ over the last time step, the probability that nodes will ever overlap and paths will be merged is increadibly small.

Futhermore, RTT performs badly in this case as trajectories are not straight and far from optimal. I could see it working a lot better where inputs have a similar effect regardless of the location, but this is not the case—jumping does nothing when already in the air, but it does something when the player is on the ground. Since RTT works by taking a random point and expanding the closest node with the action that minimizes distance, it will often having issues expanding the correct node to jump from as often the closest node to a random point will be a player who has jumped too early to reach a block instead of a player who is still on the ground but will jump soon.

Hybrid A* with Dijkstra’s as Heuristic #

I then thought what if we could use block-wise Dijkstra’s to find the minimum distance based to the goal from any point. The following illustration shows a visualization of the heuristic distance to the goal where black is close to the goal (the blue dot) and pure red is very far.

I also used Dolgov, Dmitri, et al. “Path planning for autonomous vehicles in unknown semi-structured environments.” which mentions a Hybrid A* method for holonomic systems that discretizes based on a defined grid-size and then takes the most promising node state at any $(x_i,y_j)$, where $i, j \in \mathbb{Z}$ and there is some constant $c$ such that $c(x_i, y_j) = (x,y)$. Both of these combined allows both promising nodes to be expanded (with the much better heuristic) and for the number of nodes to select from to be much smaller. Although reducing the number of nodes makes the problem solveable, it is no longer going to be optimal as we are reducing the search space.

Running, we get: